Causal Inference

class pgmpy.inference.CausalInference.CausalInference(model)

This is an inference class for performing Causal Inference over Bayesian Networks or Structural Equation Models.

Parameters:

model (pgmpy.base.DAG | pgmpy.models.DiscreteBayesianNetwork | pgmpy.models.SEMGraph) – The model that we’ll perform inference over.

Examples

Create a small Bayesian Network.

>>> from pgmpy.models import DiscreteBayesianNetwork
>>> game = DiscreteBayesianNetwork([('X', 'A'),
...                                 ('A', 'Y'),
...                                 ('A', 'B')])

Load the graph into the CausalInference object to make causal queries.

>>> from pgmpy.inference.CausalInference import CausalInference
>>> inference = CausalInference(game)
>>> inference.get_all_backdoor_adjustment_sets(X="X", Y="Y")
>>> inference.get_all_frontdoor_adjustment_sets(X="X", Y="Y")

References

‘Causality: Models, Reasoning, and Inference’ - Judea Pearl (2000)

estimate_ate(X, Y, data, estimand_strategy='smallest', estimator_type='linear', **kwargs)

Estimate the average treatment effect (ATE) of X on Y.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable

• data (pandas.DataFrame) – All observed data for this Bayesian Network.

• estimand_strategy (str or frozenset) –

  Either specify a specific backdoor adjustment set or a strategy. The available options are:

  smallest:

  Use the smallest estimand of observed variables

  all:

  Estimate the ATE from each identified estimand

• estimator_type (str) –

  The type of model to be used to estimate the ATE. All of the linear regression classes in statsmodels are available including:

  • GLS: generalized least squares for arbitrary covariance

  • OLS: ordinary least square of i.i.d. errors

  • WLS: weighted least squares for heteroskedastic error

  Specify them with their acronym (e.g. “OLS”) or simple “linear” as an alias for OLS.

• **kwargs (dict) –

  Keyward arguments specific to the selected estimator. linear:

  missing: str

  Available options are “none”, “drop”, or “raise”

Returns:

The average treatment effect

Return type:

float

Examples

>>> import pandas as pd
>>> game1 = DiscreteBayesianNetwork([('X', 'A'),
...                          ('A', 'Y'),
...                          ('A', 'B')])
>>> data = pd.DataFrame(np.random.randint(2, size=(1000, 4)), columns=['X', 'A', 'B', 'Y'])
>>> inference = CausalInference(model=game1)
>>> inference.estimate_ate("X", "Y", data=data, estimator_type="linear")

get_all_backdoor_adjustment_sets(X, Y)

Returns a list of all adjustment sets per the back-door criterion.

A set of variables Z satisfies the back-door criterion relative to an ordered pair of variabies (Xi, Xj) in a DAG G if:

1. no node in Z is a descendant of Xi; and

2. Z blocks every path between Xi and Xj that contains an arrow into Xi.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable.

Returns:

• frozenset (A frozenset of frozensets)

• Y (str) – Target Variable

Examples

>>> game1 = DiscreteBayesianNetwork([('X', 'A'),
...                          ('A', 'Y'),
...                          ('A', 'B')])
>>> inference = CausalInference(game1)
>>> inference.get_all_backdoor_adjustment_sets("X", "Y")
frozenset()

get_all_frontdoor_adjustment_sets(X, Y)

Identify possible sets of variables, Z, which satisfy the front-door criterion relative to given X and Y.

Z satisfies the front-door criterion if:

1. Z intercepts all directed paths from X to Y

2. there is no backdoor path from X to Z

3. all back-door paths from Z to Y are blocked by X

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable

Returns:

frozenset

Return type:

a frozenset of frozensets

get_conditional_ivs(X, Y, scaling_indicators={})

Returns the conditional IVs for the relation X -> Y

Parameters:

• X (node) – The observed variable’s name

• Y (node) – The oberved variable’s name

• scaling_indicators (dict (optional)) – A dict representing which observed variable to use as scaling indicator for the latent variables. If not provided, automatically finds scaling indicators by randomly selecting one of the measurement variables of each latent variable.

Returns:

set

Return type:

Set of 2-tuples representing tuple[0] is an IV for X -> Y given tuple[1].

References

[1]

Van Der Zander, B., Textor, J., & Liskiewicz, M. (2015, June). Efficiently finding conditional instruments for causal inference. In Twenty-Fourth International Joint Conference on Artificial Intelligence.

Examples

>>> from pgmpy.models import SEMGraph
>>> model = SEMGraph(ebunch=[('I', 'X'), ('X', 'Y'), ('W', 'I')],
...                  latents=[],
...                  err_corr=[('W', 'Y')])
>>> model.get_ivs('X', 'Y')
[('I', {'W'})]

get_ivs(X, Y, scaling_indicators={})

Returns the Instrumental variables(IVs) for the relation X -> Y

Parameters:

• X (node) – The variable name (observed or latent)

• Y (node) – The variable name (observed or latent)

• scaling_indicators (dict (optional)) – A dict representing which observed variable to use as scaling indicator for the latent variables. If not given the method automatically selects one of the measurement variables at random as the scaling indicator.

Returns:

set – The set of Instrumental Variables for X -> Y.

Return type:

{str}

Examples

>>> from pgmpy.models import SEMGraph
>>> model = SEMGraph(ebunch=[('I', 'X'), ('X', 'Y')],
...                  latents=[],
...                  err_corr=[('X', 'Y')])
>>> model.get_ivs('X', 'Y')
{'I'}

get_minimal_adjustment_set(X, Y)

Returns a minimal adjustment set for identifying the causal effect of X on Y.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable

Returns:

Minimal adjustment set – A set of variables which are the minimal possible adjustment set. If None, no adjustment set is possible.

Return type:

set or None

Examples

>>> from pgmpy.models import DiscreteBayesianNetwork
>>> from pgmpy.inference import CausalInference
>>> dag = DiscreteBayesianNetwork([("X_1", "X_2"), ("Z", "X_1"), ("Z", "X_2")])
>>> infer = CausalInference(dag)
>>> infer.get_minimal_adjustment_set("X_1", "X_2")
{'Z'}

References

[1] Perkovic, Emilija, et al. “Complete graphical characterization and construction of adjustment sets in Markov equivalence classes of ancestral graphs.” The Journal of Machine Learning Research 18.1 (2017): 8132-8193.

get_proper_backdoor_graph(X, Y, inplace=False)

Returns a proper backdoor graph for the exposure X and outcome Y. A proper backdoor graph is a graph which remove the first edge of every proper causal path from X to Y.

Parameters:

• X (list (array-like)) – A list of exposure variables.

• Y (list (array-like)) – A list of outcome variables

• inplace (boolean) – If inplace is True, modifies the object itself. Otherwise retuns a modified copy of self.

Examples

>>> from pgmpy.models import DiscreteBayesianNetwork
>>> from pgmpy.inference import CausalInference
>>> model = DiscreteBayesianNetwork([("x1", "y1"), ("x1", "z1"), ("z1", "z2"),
...                        ("z2", "x2"), ("y2", "z2")])
>>> c_infer = CausalInference(model)
>>> c_infer.get_proper_backdoor_graph(X=["x1", "x2"], Y=["y1", "y2"])
<pgmpy.models.DiscreteBayesianNetwork.DiscreteBayesianNetwork at 0x7fba501ad940>

References

[1] Perkovic, Emilija, et al. “Complete graphical characterization and construction of adjustment sets in Markov equivalence classes of ancestral graphs.” The Journal of Machine Learning Research 18.1 (2017): 8132-8193.

get_scaling_indicators()

Returns a scaling indicator for each of the latent variables in the model. The scaling indicator is chosen randomly among the observed measurement variables of the latent variable.

Examples

>>> from pgmpy.models import SEMGraph
>>> model = SEMGraph(ebunch=[('xi1', 'eta1'), ('xi1', 'x1'), ('xi1', 'x2'),
...                          ('eta1', 'y1'), ('eta1', 'y2')],
...                  latents=['xi1', 'eta1'])
>>> model.get_scaling_indicators()
{'xi1': 'x1', 'eta1': 'y1'}

Returns:

dict – scaling indicator.

Return type:

Returns a dict with latent variables as the key and their value being the

identification_method(X, Y)

Automatically identifies a valid method for estimating the causal effect from X to Y.

Parameters:

• X (str) – The treatment/exposure variable

• Y (str) – The outcome variable

Returns:

A dictionary containing keys as method and value as the corresponding result.

Return type:

dict

is_valid_adjustment_set(X, Y, adjustment_set)

Method to test whether adjustment_set is a valid adjustment set for identifying the causal effect of X on Y.

Parameters:

• X (list (array-like)) – The set of cause variables.

• Y (list (array-like)) – The set of predictor variables.

• adjustment_set (list (array-like)) – The set of variables for which to test whether they satisfy the adjustment set criteria.

Returns:

Is valid adjustment set – Returns True if adjustment_set is a valid adjustment set for identifying the effect of X on Y. Else returns False.

Return type:

bool

Examples

>>> from pgmpy.models import DiscreteBayesianNetwork
>>> from pgmpy.inference import CausalInference
>>> model = DiscreteBayesianNetwork([("x1", "y1"), ("x1", "z1"), ("z1", "z2"),
...                        ("z2", "x2"), ("y2", "z2")])
>>> c_infer = CausalInference(model)
>>> c_infer.is_valid_adjustment_set(X=['x1', 'x2'], Y=['y1', 'y2'], adjustment_set=['z1', 'z2'])
True

References

[1] Perkovic, Emilija, et al. “Complete graphical characterization and construction of adjustment sets in Markov equivalence classes of ancestral graphs.” The Journal of Machine Learning Research 18.1 (2017): 8132-8193.

is_valid_backdoor_adjustment_set(X, Y, Z=[])

Test whether Z is a valid backdoor adjustment set for estimating the causal impact of X on Y.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable.

• Z (list (array-like)) – List of adjustment variables.

Returns:

Is a valid backdoor adjustment set – True if Z is a valid backdoor adjustment set else False

Return type:

bool

Examples

>>> game1 = DiscreteBayesianNetwork([('X', 'A'),
...                          ('A', 'Y'),
...                          ('A', 'B')])
>>> inference = CausalInference(game1)
>>> inference.is_valid_backdoor_adjustment_set("X", "Y")
True

is_valid_frontdoor_adjustment_set(X, Y, Z=None)

Test whether Z is a valid frontdoor adjustment set for estimating the causal impact of X on Y via the frontdoor adjustment formula.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable.

• Z (list (array-like)) – List of adjustment variables.

Returns:

Is valid frontdoor adjustment – True if Z is a valid frontdoor adjustment set.

Return type:

bool

query(variables, do=None, evidence=None, adjustment_set=None, inference_algo='ve', show_progress=True, **kwargs)

Performs a query on the model of the form 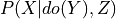where 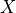is variables, 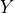is do and Z is the evidence.

Parameters:

• variables (list) – list of variables in the query i.e. X in .

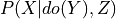• do (dict (default: None)) – Dictionary of the form {variable_name: variable_state} representing the variables on which to apply the do operation i.e. Y in .

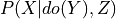• evidence (dict (default: None)) – Dictionary of the form {variable_name: variable_state} repesenting the conditional variables in the query i.e. Z in .

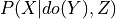• adjustment_set (str or list (default=None)) – Specifies the adjustment set to use. If None, uses the parents of the do variables as the adjustment set.

• inference_algo (str or pgmpy.inference.Inference instance) – The inference algorithm to use to compute the probability values. String options are: 1) ve: Variable Elimination 2) bp: Belief Propagation.

• kwargs (Any) – Additional paramters which needs to be passed to inference algorithms. Please refer to the pgmpy.inference.Inference for details.

Returns:

Queried distribution – A factor object representing the joint distribution over the variables in variables.

Return type:

pgmpy.factor.discrete.DiscreteFactor

Examples

>>> from pgmpy.utils import get_example_model
>>> model = get_example_model('alarm')
>>> infer = CausalInference(model)
>>> infer.query(['HISTORY'], do={'CVP': 'LOW'}, evidence={'HR': 'LOW'})
<DiscreteFactor representing phi(HISTORY:2) at 0x7f4e0874c2e0>