Causal Inference

class pgmpy.inference.CausalInference.CausalInference(model, set_nodes=None)

This is an inference class for performing Causal Inference over Bayesian Networks or Structural Equation Models.

Parameters:

• model (pgmpy.base.DAG | pgmpy.models.DiscreteBayesianNetwork) – The model that we’ll perform inference over.

• set_nodes (list[node:str] or None) – A list (or set/tuple) of nodes in the Bayesian Network which have been set to a specific value per the do-operator.

Examples

Create a small Bayesian Network.

>>> from pgmpy.models import DiscreteBayesianNetwork
>>> game = DiscreteBayesianNetwork([('X', 'A'),
...                         ('A', 'Y'),
...                         ('A', 'B')])

Load the graph into the CausalInference object to make causal queries.

>>> from pgmpy.inference.CausalInference import CausalInference
>>> inference = CausalInference(game)
>>> inference.get_all_backdoor_adjustment_sets(X="X", Y="Y")
>>> inference.get_all_frontdoor_adjustment_sets(X="X", Y="Y")

References

‘Causality: Models, Reasoning, and Inference’ - Judea Pearl (2000)

estimate_ate(X, Y, data, estimand_strategy='smallest', estimator_type='linear', **kwargs)

Estimate the average treatment effect (ATE) of X on Y.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable

• data (pandas.DataFrame) – All observed data for this Bayesian Network.

• estimand_strategy (str or frozenset) –

  Either specify a specific backdoor adjustment set or a strategy. The available options are:

  smallest:

  Use the smallest estimand of observed variables

  all:

  Estimate the ATE from each identified estimand

• estimator_type (str) –

  The type of model to be used to estimate the ATE. All of the linear regression classes in statsmodels are available including:

  • GLS: generalized least squares for arbitrary covariance

  • OLS: ordinary least square of i.i.d. errors

  • WLS: weighted least squares for heteroskedastic error

  Specify them with their acronym (e.g. “OLS”) or simple “linear” as an alias for OLS.

• **kwargs (dict) –

  Keyward arguments specific to the selected estimator. linear:

  missing: str

  Available options are “none”, “drop”, or “raise”

Returns:

The average treatment effect

Return type:

float

Examples

>>> import pandas as pd
>>> game1 = DiscreteBayesianNetwork([('X', 'A'),
...                          ('A', 'Y'),
...                          ('A', 'B')])
>>> data = pd.DataFrame(np.random.randint(2, size=(1000, 4)), columns=['X', 'A', 'B', 'Y'])
>>> inference = CausalInference(model=game1)
>>> inference.estimate_ate("X", "Y", data=data, estimator_type="linear")

get_all_backdoor_adjustment_sets(X, Y)

Returns a list of all adjustment sets per the back-door criterion.

A set of variables Z satisfies the back-door criterion relative to an ordered pair of variabies (Xi, Xj) in a DAG G if:

1. no node in Z is a descendant of Xi; and

2. Z blocks every path between Xi and Xj that contains an arrow into Xi.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable.

Returns:

• frozenset (A frozenset of frozensets)

• Y (str) – Target Variable

Examples

>>> game1 = DiscreteBayesianNetwork([('X', 'A'),
...                          ('A', 'Y'),
...                          ('A', 'B')])
>>> inference = CausalInference(game1)
>>> inference.get_all_backdoor_adjustment_sets("X", "Y")
frozenset()

get_all_frontdoor_adjustment_sets(X, Y)

Identify possible sets of variables, Z, which satisfy the front-door criterion relative to given X and Y.

Z satisfies the front-door criterion if:

1. Z intercepts all directed paths from X to Y

2. there is no backdoor path from X to Z

3. all back-door paths from Z to Y are blocked by X

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable

Returns:

frozenset

Return type:

a frozenset of frozensets

get_minimal_adjustment_set(X, Y)

Returns a minimal adjustment set for identifying the causal effect of X on Y.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable

Returns:

Minimal adjustment set – A set of variables which are the minimal possible adjustment set. If None, no adjustment set is possible.

Return type:

set or None

Examples

>>> from pgmpy.models import DiscreteBayesianNetwork
>>> from pgmpy.inference import CausalInference
>>> dag = DiscreteBayesianNetwork([("X_1", "X_2"), ("Z", "X_1"), ("Z", "X_2")])
>>> infer = CausalInference(dag)
>>> infer.get_minimal_adjustment_set("X_1", "X_2")
{'Z'}

References

[1] Perkovic, Emilija, et al. “Complete graphical characterization and construction of adjustment sets in Markov equivalence classes of ancestral graphs.” The Journal of Machine Learning Research 18.1 (2017): 8132-8193.

get_proper_backdoor_graph(X, Y, inplace=False)

Returns a proper backdoor graph for the exposure X and outcome Y. A proper backdoor graph is a graph which remove the first edge of every proper causal path from X to Y.

Parameters:

• X (list (array-like)) – A list of exposure variables.

• Y (list (array-like)) – A list of outcome variables

• inplace (boolean) – If inplace is True, modifies the object itself. Otherwise retuns a modified copy of self.

Examples

>>> from pgmpy.models import DiscreteBayesianNetwork
>>> from pgmpy.inference import CausalInference
>>> model = DiscreteBayesianNetwork([("x1", "y1"), ("x1", "z1"), ("z1", "z2"),
...                        ("z2", "x2"), ("y2", "z2")])
>>> c_infer = CausalInference(model)
>>> c_infer.get_proper_backdoor_graph(X=["x1", "x2"], Y=["y1", "y2"])
<pgmpy.models.DiscreteBayesianNetwork.DiscreteBayesianNetwork at 0x7fba501ad940>

References

[1] Perkovic, Emilija, et al. “Complete graphical characterization and construction of adjustment sets in Markov equivalence classes of ancestral graphs.” The Journal of Machine Learning Research 18.1 (2017): 8132-8193.

is_valid_adjustment_set(X, Y, adjustment_set)

Method to test whether adjustment_set is a valid adjustment set for identifying the causal effect of X on Y.

Parameters:

• X (list (array-like)) – The set of cause variables.

• Y (list (array-like)) – The set of predictor variables.

• adjustment_set (list (array-like)) – The set of variables for which to test whether they satisfy the adjustment set criteria.

Returns:

Is valid adjustment set – Returns True if adjustment_set is a valid adjustment set for identifying the effect of X on Y. Else returns False.

Return type:

bool

Examples

>>> from pgmpy.models import DiscreteBayesianNetwork
>>> from pgmpy.inference import CausalInference
>>> model = DiscreteBayesianNetwork([("x1", "y1"), ("x1", "z1"), ("z1", "z2"),
...                        ("z2", "x2"), ("y2", "z2")])
>>> c_infer = CausalInference(model)
>>> c_infer.is_valid_adjustment_set(X=['x1', 'x2'], Y=['y1', 'y2'], adjustment_set=['z1', 'z2'])
True

References

[1] Perkovic, Emilija, et al. “Complete graphical characterization and construction of adjustment sets in Markov equivalence classes of ancestral graphs.” The Journal of Machine Learning Research 18.1 (2017): 8132-8193.

is_valid_backdoor_adjustment_set(X, Y, Z=[])

Test whether Z is a valid backdoor adjustment set for estimating the causal impact of X on Y.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable.

• Z (list (array-like)) – List of adjustment variables.

Returns:

Is a valid backdoor adjustment set – True if Z is a valid backdoor adjustment set else False

Return type:

bool

Examples

>>> game1 = DiscreteBayesianNetwork([('X', 'A'),
...                          ('A', 'Y'),
...                          ('A', 'B')])
>>> inference = CausalInference(game1)
>>> inference.is_valid_backdoor_adjustment_set("X", "Y")
True

is_valid_frontdoor_adjustment_set(X, Y, Z=None)

Test whether Z is a valid frontdoor adjustment set for estimating the causal impact of X on Y via the frontdoor adjustment formula.

Parameters:

• X (str (variable name)) – The cause/exposure variables.

• Y (str (variable name)) – The outcome variable.

• Z (list (array-like)) – List of adjustment variables.

Returns:

Is valid frontdoor adjustment – True if Z is a valid frontdoor adjustment set.

Return type:

bool

query(variables, do=None, evidence=None, adjustment_set=None, inference_algo='ve', show_progress=True, **kwargs)

Performs a query on the model of the form 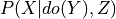where 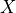is variables, 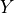is do and Z is the evidence.

Parameters:

• variables (list) – list of variables in the query i.e. X in .

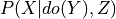• do (dict (default: None)) – Dictionary of the form {variable_name: variable_state} representing the variables on which to apply the do operation i.e. Y in .

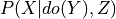• evidence (dict (default: None)) – Dictionary of the form {variable_name: variable_state} repesenting the conditional variables in the query i.e. Z in .

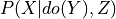• adjustment_set (str or list (default=None)) – Specifies the adjustment set to use. If None, uses the parents of the do variables as the adjustment set.

• inference_algo (str or pgmpy.inference.Inference instance) – The inference algorithm to use to compute the probability values. String options are: 1) ve: Variable Elimination 2) bp: Belief Propagation.

• kwargs (Any) – Additional paramters which needs to be passed to inference algorithms. Please refer to the pgmpy.inference.Inference for details.

Returns:

Queried distribution – A factor object representing the joint distribution over the variables in variables.

Return type:

pgmpy.factor.discrete.DiscreteFactor

Examples

>>> from pgmpy.utils import get_example_model
>>> model = get_example_model('alarm')
>>> infer = CausalInference(model)
>>> infer.query(['HISTORY'], do={'CVP': 'LOW'}, evidence={'HR': 'LOW'})
<DiscreteFactor representing phi(HISTORY:2) at 0x7f4e0874c2e0>