Factor Graph¶
- class pgmpy.models.FactorGraph.FactorGraph(ebunch=None)[source]¶
Class for representing factor graph.
DiscreteFactor graph is a bipartite graph representing factorization of a function. They allow efficient computation of marginal distributions through sum-product algorithm.
A factor graph contains two types of nodes. One type corresponds to random variables whereas the second type corresponds to factors over these variables. The graph only contains edges between variables and factor nodes. Each factor node is associated with one factor whose scope is the set of variables that are its neighbors.
- Parameters:
data (input graph) – Data to initialize graph. If data=None (default) an empty graph is created. The data is an edge list.
Examples
Create an empty FactorGraph with no nodes and no edges
>>> from pgmpy.models import FactorGraph >>> G = FactorGraph()
G can be grown by adding variable nodes as well as factor nodes
Nodes:
Add a node at a time or a list of nodes.
>>> G.add_node("a") >>> G.add_nodes_from(["a", "b"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> G.add_factors(phi1) >>> G.add_nodes_from([phi1])
Edges:
G can also be grown by adding edges.
>>> G.add_edge("a", phi1)
or a list of edges
>>> G.add_edges_from([("a", phi1), ("b", phi1)])
- add_edge(u, v, **kwargs)[source]¶
Add an edge between variable_node and factor_node.
- Parameters:
u (nodes) – Nodes can be any hashable Python object.
v (nodes) – Nodes can be any hashable Python object.
Examples
>>> from pgmpy.models import FactorGraph >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> G.add_nodes_from([phi1]) >>> G.add_edge("a", phi1)
- add_factors(*factors, replace=False)[source]¶
Associate a factor to the graph. See factors class for the order of potential values.
- Parameters:
*factor (pgmpy.factors.DiscreteFactor object) – A factor object on any subset of the variables of the model which is to be associated with the model.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_factors(phi1, phi2) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)])
- check_model()[source]¶
Check the model for various errors. This method checks for the following errors. In the same time it also updates the cardinalities of all the random variables.
Check whether bipartite property of factor graph is still maintained or not.
Check whether factors are associated for all the random variables or not.
Check if factors are defined for each factor node or not.
Check if cardinality information for all the variables is available or not.
Check if cardinality of random variable remains same across all the factors.
- copy()[source]¶
Returns a copy of the model.
- Returns:
FactorGraph
- Return type:
Copy of FactorGraph
Examples
>>> import numpy as np >>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_factors(phi1, phi2) >>> G.add_nodes_from([phi1, phi2]) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)]) >>> G_copy = G.copy() >>> G_copy.nodes() NodeView((<Factor representing phi(b:2, c:2) at 0xb4badd4c>, 'b', 'c', 'a', <Factor representing phi(a:2, b:2) at 0xb4badf2c>))
- get_cardinality(node=None)[source]¶
Returns the cardinality of the node
- Parameters:
node (any hashable python object (optional)) – The node whose cardinality we want. If node is not specified returns a dictionary with the given variable as keys and their respective cardinality as values.
- Returns:
int or dict – If node is not specified returns a dictionary with the given variable as keys and their respective cardinality as values.
- Return type:
If node is specified returns the cardinality of the node.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_nodes_from([phi1, phi2]) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)]) >>> G.add_factors(phi1, phi2) >>> G.get_cardinality() defaultdict(<class 'int'>, {'c': 2, 'b': 2, 'a': 2})
>>> G.get_cardinality("a") 2
- get_factor_nodes()[source]¶
Returns factors nodes present in the graph.
Before calling this method make sure that all the factors are added properly.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_nodes_from([phi1, phi2]) >>> G.add_factors(phi1, phi2) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)]) >>> G.get_factor_nodes() [<DiscreteFactor representing phi(b:2, c:2) at 0x4b8c7f0>, <DiscreteFactor representing phi(a:2, b:2) at 0x4b8c5b0>]
- get_factors(node=None)[source]¶
Returns the factors that have been added till now to the graph.
If node is not None, it would return the factor corresponding to the given node.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_factors(phi1, phi2) >>> G.add_nodes_from([phi1, phi2]) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)]) >>> G.get_factors() >>> G.get_factors(node=phi1)
- get_partition_function()[source]¶
Returns the partition function for a given undirected graph.
A partition function is defined as
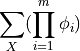
where m is the number of factors present in the graph and X are all the random variables present.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_factors(phi1, phi2) >>> G.add_nodes_from([phi1, phi2]) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)]) >>> G.get_factors() >>> G.get_partition_function()
- get_point_mass_message(variable, observation)[source]¶
Returns a point mass message for the variable given the observed state.
- Parameters:
variable (str) – The variable for which the message needs to be computed.
observation (int) – The observed state of the variable.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_node("a") >>> phi = DiscreteFactor(["a"], [4], np.random.rand(4)) >>> G.add_factors(phi) >>> G.add_edges_from([("a", phi)]) >>> G.get_point_mass_message("a", 1) array([0, 1, 0, 0])
- get_uniform_message(variable)[source]¶
Returns a uniform message for the given variable
- Parameters:
variable (str) – The variable for which the message needs to be computed.
Examples
>>> from pgmpy.models import FactorGraph >>> G = FactorGraph() >>> G.add_node("a") >>> phi = DiscreteFactor(["a"], [4], np.random.rand(4)) >>> G.add_factors(phi) >>> G.add_edges_from([("a", phi)]) >>> G.get_get_uniform_message("a") array([0.25, 0.25, 0.25, 0.25])
- get_variable_nodes()[source]¶
Returns variable nodes present in the graph.
Before calling this method make sure that all the factors are added properly.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_nodes_from([phi1, phi2]) >>> G.add_factors(phi1, phi2) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)]) >>> G.get_variable_nodes() ['a', 'c', 'b']
- remove_factors(*factors)[source]¶
Removes the given factors from the added factors.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> G.add_factors(phi1) >>> G.remove_factors(phi1)
- to_junction_tree()[source]¶
Create a junction treeo (or clique tree) for a given factor graph.
For a given factor graph (H) a junction tree (G) is a graph 1. where each node in G corresponds to a maximal clique in H 2. each sepset in G separates the variables strictly on one side of edge to other
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_factors(phi1, phi2) >>> G.add_nodes_from([phi1, phi2]) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)]) >>> mm = G.to_markov_model()
- to_markov_model()[source]¶
Converts the factor graph into markov model.
A markov model contains nodes as random variables and edge between two nodes imply interaction between them.
Examples
>>> from pgmpy.models import FactorGraph >>> from pgmpy.factors.discrete import DiscreteFactor >>> G = FactorGraph() >>> G.add_nodes_from(["a", "b", "c"]) >>> phi1 = DiscreteFactor(["a", "b"], [2, 2], np.random.rand(4)) >>> phi2 = DiscreteFactor(["b", "c"], [2, 2], np.random.rand(4)) >>> G.add_factors(phi1, phi2) >>> G.add_nodes_from([phi1, phi2]) >>> G.add_edges_from([("a", phi1), ("b", phi1), ("b", phi2), ("c", phi2)]) >>> mm = G.to_markov_model()
