Linear Gaussian CPD

class pgmpy.factors.continuous.LinearGaussianCPD.LinearGaussianCPD(variable, beta, std, evidence=[])

Defines a Linear Gaussian CPD.

The Linear Gaussian CPD makes the following assumptions:

1. The variable is Gaussian/Normally distributed.

2. The mean of the variable depends on the values of the parents and the

   intercept term.

3. The variance is independent of other variables.

For example,

p(Y|X) = N(0.9 - 2x; 1)

Here, 0.9 - 2x is the mean of the variable 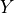and the standard deviation is 1.

In generalized terms, let 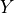be a Gaussian variable with parents X_1, X_2, \cdots, X_k. Assuming linear relationship between Y and mathbf{X}, the conditional distribution of Y can be defined as:

p(Y |x1, x2, ..., xk) = \mathcal{N}(\beta_0 + x1*\beta_1 + ......... + xk*\beta_k ; \sigma)

References

[1]

https://cedar.buffalo.edu/~srihari/CSE574/Chap8/Ch8-PGM-GaussianBNs/8.5%20GaussianBNs.pdf

Parameters:

• variable (any hashable python object) – The variable whose CPD is defined.

• beta (list (array-like)) – The coefficients corresponding to each of the evidence variable. The first term of the beta array is the intercept term.

• std (float) – The standard deviation of variable.

• evidence (iterator (array-like)) – List of parents/evidence variables of variable. The order in which evidence is specified should match the order of beta.

Examples

# To represent the conditional distribution, P(Y| X1, X2, X3) = N(0.2 - 2*x1 + 3*x2 + 7*x3 ; 9.6), we can write:

>>> from pgmpy.factors.continuous import LinearGaussianCPD
>>> cpd = LinearGaussianCPD('Y',  [0.2, -2, 3, 7], 9.6, ['X1', 'X2', 'X3'])
>>> cpd.variable
'Y'
>>> cpd.evidence
['x1', 'x2', 'x3']
>>> cpd.beta_vector
[0.2, -2, 3, 7]

copy()

Returns a copy of the distribution.

Returns:

LinearGaussianCPD

Return type:

copy of the distribution

Examples

>>> from pgmpy.factors.continuous import LinearGaussianCPD
>>> cpd = LinearGaussianCPD('Y',  [0.2, -2, 3, 7], 9.6, ['X1', 'X2', 'X3'])
>>> copy_cpd = cpd.copy()
>>> copy_cpd.variable
'Y'
>>> copy_cpd.evidence
['X1', 'X2', 'X3']

static get_random(variable, evidence, loc=0.0, scale=1.0, seed=None)

Generates a LinearGaussianCPD instance with random values on variable with parents/evidence evidence with beta and std sampled from loc and scale

Parameters:

• variable (str, int or any hashable python object.) – The variable on which to define the TabularCPD.

• evidence (list, array-like) – A list of variable names which are the parents/evidence of variable.

• loc (float) – The mean of the normal distribution from which the coefficients are sampled.

• scale (float) – The standard deviation of the normal distribution from which the coefficients are sampled.

• seed (int (default: None)) – The seed for the random number generator.

Returns:

Random CPD – A LinearGaussianCPD object on variable with evidence as evidence with random values.

Return type:

pgmpy.factors.continuous.LinearGaussianCPD

Examples

>>> from pgmpy.factors.continuous import LinearGaussianCPD
>>> LinearGaussianCPD.get_random(variable='Income', evidence=['Age', 'Experience'],
...            loc=2.0, scale=0.5, seed=5)
<LinearGaussianCPD: P(Income | Age, Experience) = N(1.338*Age + 1.876*Experience + 1.599; 2.21) at 0x1795561e0