A Bayesian Network to model the influence of energy consumption on greenhouse gases in Italy

by Lorenzo Mario Amorosa

Fundamentals of Artificial Intelligence and Knowledge Representation (Mod. 3) - Alma Mater Studiorum Università di Bologna

Abstract

|f559beb584fb457f81121bd122784167| Nowadays it is well established that global warming is hugely caused by greenhouse gases, which are indeed responsible for trapping heat in the atmosphere. The 3 most common gases are carbon dioxide (CO2), methane (CH4) and nitrous oxide (N2O) [1].

There are several sources of greenhouse gases, such as transportation, industry, commercial and residental. In this document I will tackle the problem in a general way, considering the impact of energy consumption on greenhouse gases emissions. Energy is indeed strictly related to almost all source factors. In particular, I will face the modelling of causal relations between energy consumption and greenhouse gases in Italy using a Bayesian network. The aim is to learn a model that can provide probabilistic results given some input evidence. The causal relations and their relative probabilities will be estimated by analyzing annual growth factors of several indicators from open source datasets of the World Bank Group (WBG) [3]. The choice of analyzing the annual growth aims to capture how the variation of an indicator can affect the others.

This work starts from a paper by Cinar and Kayakutlu (2010) [2] in which the authors produced estimates about energy investments in Turkey given historical data. Their work helped me to come up with interesting measures to be investigated and to be represented in the Bayesian network. I could extend their work adding: a more comprehensive analysis of network properties (conditional independencies, active trails, Markov blankets), concise and effective high level functions (such as query_report, check_assertion and active_trails_of) to express the most significant properties in a readable format and the whole code to learn the Bayesian network from the available datasets.

Network definition

Generally we can expect that the increase of fossil fuel consumption determines the growth of greenhouse gases diffusion, whereas a wider use of renewable energies leads to a reduction of greenhouse gases emissions. In [2] it is suggested that growth rate factors about population, urbanization and gross domestic product (GDP) can all influence the overall energy use in a nation. Given these assumptions, the Bayesian network is defined as follows: |ea95c40f81784daeaecf2a9ee1bd0f7b| The terms in the nodes have the following labels in [3]:

Pop = Population growth (annual %)

Urb = Urban population growth (annual %)

GDP = GDP per capita growth (annual %)

EC = Energy use (kg of oil equivalent per capita) - [annual growth %]

FFEC = Fossil fuel energy consumption (% of total) - [annual growth %]

REC = Renewable energy consumption (% of total final energy consumption) - [annual growth %]

EI = Energy imports, net (% of energy use) - [annual growth %]

CO2 = CO2 emissions (metric tons per capita) - [annual growth %]

CH4 = Methane emissions in energy sector (thousand metric tons of CO2 equivalent) - [annual growth %]

N2O = Nitrous oxide emissions in energy sector (thousand metric tons of CO2 equivalent) - [annual growth %]

The Bayesian network proposed differs from the one of [2] because here greenhouse gases are kept distinct (CO2, CH4, N2O) and energy investments are not represented.

In the following cell the Bayesian network is created using the pgmpy library.

from pgmpy.models import BayesianModel

model = BayesianModel([('Pop', 'EC'),   ('Urb', 'EC'),   ('GDP', 'EC'),
                       ('EC', 'FFEC'),  ('EC', 'REC'),   ('EC', 'EI'),
                       ('REC', 'CO2'),  ('REC', 'CH4'),  ('REC', 'N2O'),
                       ('FFEC', 'CO2'), ('FFEC', 'CH4'), ('FFEC', 'N2O')])

Datasets

The data to compute the conditional probability tables (CPT) of the network are retrived from [3]. Some data are given there in absolute values and not in terms of annual growth, hence it is necessary to transform them properly (the labels of transformed data are marked with the trailing string “- [annual growth %]”).

A good methodology to organize historical data to infer CPT, as shown also in [2], is to group them by year, such that historical values of the same year are treated as a single tuple and thus they constitute a whole entry of the dataset. Data discretization is also needed, since pgmpy does not support learning from continuous variables, and so all values are mapped into 3 fixed tiers. In order to minimize data sparsity, the boundaries of the mapping intervals are chosen such that each tier of the same node contains an equal number of samples.

The pgmpy learning algorithms expect as input a dataframe in which each entry represents an observed event — a year in this case. As a consequence some data preprocessing is needed to make the raw data compatible with the required signature. It is worth noting that pgmpy handles learning task with sparse datasets (i.e. it handles NaN values). To compute indeed the CPT for a given node in the network there are used only those entries in which both the node itself and its parents are defined (i.e. an entry is used to compute a given CPT only if all needed values of that year are defined). This fact implies that the deeper the network is, the less sparse the dataset should be to compute significant CPT.

As a side note, mind the fact that industrialization growth, which is expressed by indicators such as industry value added, is not represented in the newtork. Data regarding industrialization are available only for a short year range in [3] and the industrialization node would be on top of the network hierarchy, being a parent of the node ‘EC’. As a consequence, if industrialization would be represented, then the overall learning process could rely only on a small subset of all the available data and the network parameters would be estimated less significantly.

In the following cells data are imported and preprocessed.

Raw data

from pandas import read_csv, DataFrame
import numpy as np

def annual_growth(row, years):
    min_year = years["min"]
    max_year = years["max"]
    row["Indicator Name"] = row["Indicator Name"] + " - [annual growth %]"
    for year in range(max_year, min_year, -1):
        if not np.isnan(row[str(year)]) and not np.isnan(row[str(year - 1)]):
            row[str(year)] = 100 * (float(row[str(year)]) - float(row[str(year - 1)])) / abs(float(row[str(year - 1)]))
        else:
            row[str(year)] = np.nan
    row[str(min_year)] = np.nan
    return row

years = {"min" : 1960, "max" : 2019}
df_raw = read_csv("../csv/italy-raw-data.csv")
df_raw_growth = DataFrame(data=[row if "growth" in row["Indicator Name"] else annual_growth(row, years) for index, row in df_raw.iterrows()])
print("There are " + str(df_raw_growth.shape[0]) + " indicators in the dataframe.")
df_raw_growth.head()

There are 10 indicators in the dataframe.

	Country Name	Country Code	Indicator Name	Indicator Code	1960	1961	1962	1963	1964	1965	...	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019
0	Italy	ITA	Population growth (annual %)	SP.POP.GROW	1.993928	0.668383	0.676623	0.729553	0.822624	0.842109	...	0.307591	0.171978	0.269541	1.159251	0.917504	-0.096376	-0.169884	-0.149861	-0.190064	NaN
1	Italy	ITA	Urban population growth (annual %)	SP.URB.GROW	2.836401	1.498807	1.506833	1.551287	1.636027	1.642485	...	0.480439	0.343066	0.619579	1.587835	1.341371	0.325701	0.246127	0.262999	0.228198	NaN
2	Italy	ITA	GDP per capita growth (annual %)	NY.GDP.PCAP.KD.ZG	NaN	7.486419	5.487478	4.842052	1.955533	2.402046	...	1.400915	0.534287	-3.242060	-2.972404	-0.917814	0.875477	1.451875	1.868715	0.966058	NaN
3	Italy	ITA	Energy use (kg of oil equivalent per capita) -...	EG.USE.PCAP.KG.OE	NaN	12.062200	13.064053	11.188621	9.110076	7.753922	...	2.113919	-3.486796	-4.211107	-4.791839	-6.396212	2.786129	NaN	NaN	NaN	NaN
4	Italy	ITA	Fossil fuel energy consumption (% of total) - ...	EG.USE.COMM.FO.ZS	NaN	2.344018	1.933224	-0.167728	1.075163	-0.074481	...	-0.262284	-0.193760	-2.679745	-2.721392	-1.723158	1.733165	NaN	NaN	NaN	NaN

5 rows × 64 columns

Data cleaning

nodes = ['Pop', 'Urb', 'GDP', 'EC', 'FFEC', 'REC', 'EI', 'CO2', 'CH4', 'N2O']
df_growth = df_raw_growth.transpose().iloc[4:]
df_growth.columns = nodes
df_growth.head(10)

	Pop	Urb	GDP	EC	FFEC	REC	EI	CO2	CH4	N2O
1960	1.99393	2.8364	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1961	0.668383	1.49881	7.48642	12.0622	2.34402	NaN	5.07261	13.8924	NaN	NaN
1962	0.676623	1.50683	5.48748	13.0641	1.93322	NaN	5.75395	17.5887	NaN	NaN
1963	0.729553	1.55129	4.84205	11.1886	-0.167728	NaN	2.51943	12.5116	NaN	NaN
1964	0.822624	1.63603	1.95553	9.11008	1.07516	NaN	0.631028	6.78298	NaN	NaN
1965	0.842109	1.64248	2.40205	7.75392	-0.0744814	NaN	2.33506	7.84845	NaN	NaN
1966	0.777304	1.56811	5.16416	8.70603	0.552096	NaN	1.51847	12.9005	NaN	NaN
1967	0.723778	1.50361	6.40568	8.41638	1.19174	NaN	1.938	9.41875	NaN	NaN
1968	0.631737	1.40395	5.87359	9.46868	0.880322	NaN	1.59627	6.42744	NaN	NaN
1969	0.566059	1.32609	5.49918	7.89391	0.940778	NaN	0.725698	8.22188	NaN	NaN

Data discretization

TIERS_NUM = 3

def boundary_str(start, end, tier):
    return f'{tier}: {start:+0,.2f} to {end:+0,.2f}'

def relabel(v, boundaries):
    if v >= boundaries[0][0] and v <= boundaries[0][1]:
        return boundary_str(boundaries[0][0], boundaries[0][1], tier='A')
    elif v >= boundaries[1][0] and v <= boundaries[1][1]:
        return boundary_str(boundaries[1][0], boundaries[1][1], tier='B')
    elif v >= boundaries[2][0] and v <= boundaries[2][1]:
        return boundary_str(boundaries[2][0], boundaries[2][1], tier='C')
    else:
        return np.nan

def get_boundaries(tiers):
    prev_tier = tiers[0]
    boundaries = [(prev_tier[0], prev_tier[prev_tier.shape[0] - 1])]
    for index, tier in enumerate(tiers):
        if index is not 0:
            boundaries.append((prev_tier[prev_tier.shape[0] - 1], tier[tier.shape[0] - 1]))
            prev_tier = tier
    return boundaries

new_columns = {}
for i, content in enumerate(df_growth.items()):
    (label, series) = content
    values = np.sort(np.array([x for x in series.tolist() if not np.isnan(x)] , dtype=float))
    if values.shape[0] < TIERS_NUM:
        print(f'Error: there are not enough data for label {label}')
        break
    boundaries = get_boundaries(tiers=np.array_split(values, TIERS_NUM))
    new_columns[label] = [relabel(value, boundaries) for value in series.tolist()]

df = DataFrame(data=new_columns)
df.columns = nodes
df.index = range(years["min"], years["max"] + 1)
df.head(10)

	Pop	Urb	GDP	EC	FFEC	REC	EI	CO2	CH4	N2O
1960	C: +0.50 to +1.99	C: +0.82 to +2.84	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1961	C: +0.50 to +1.99	C: +0.82 to +2.84	C: +2.89 to +7.49	C: +2.79 to +13.06	C: +0.16 to +2.34	NaN	C: +0.78 to +5.75	C: +3.81 to +17.59	NaN	NaN
1962	C: +0.50 to +1.99	C: +0.82 to +2.84	C: +2.89 to +7.49	C: +2.79 to +13.06	C: +0.16 to +2.34	NaN	C: +0.78 to +5.75	C: +3.81 to +17.59	NaN	NaN
1963	C: +0.50 to +1.99	C: +0.82 to +2.84	C: +2.89 to +7.49	C: +2.79 to +13.06	B: -0.40 to +0.16	NaN	C: +0.78 to +5.75	C: +3.81 to +17.59	NaN	NaN
1964	C: +0.50 to +1.99	C: +0.82 to +2.84	B: +1.24 to +2.89	C: +2.79 to +13.06	C: +0.16 to +2.34	NaN	B: -0.38 to +0.78	C: +3.81 to +17.59	NaN	NaN
1965	C: +0.50 to +1.99	C: +0.82 to +2.84	B: +1.24 to +2.89	C: +2.79 to +13.06	B: -0.40 to +0.16	NaN	C: +0.78 to +5.75	C: +3.81 to +17.59	NaN	NaN
1966	C: +0.50 to +1.99	C: +0.82 to +2.84	C: +2.89 to +7.49	C: +2.79 to +13.06	C: +0.16 to +2.34	NaN	C: +0.78 to +5.75	C: +3.81 to +17.59	NaN	NaN
1967	C: +0.50 to +1.99	C: +0.82 to +2.84	C: +2.89 to +7.49	C: +2.79 to +13.06	C: +0.16 to +2.34	NaN	C: +0.78 to +5.75	C: +3.81 to +17.59	NaN	NaN
1968	C: +0.50 to +1.99	C: +0.82 to +2.84	C: +2.89 to +7.49	C: +2.79 to +13.06	C: +0.16 to +2.34	NaN	C: +0.78 to +5.75	C: +3.81 to +17.59	NaN	NaN
1969	C: +0.50 to +1.99	C: +0.82 to +2.84	C: +2.89 to +7.49	C: +2.79 to +13.06	C: +0.16 to +2.34	NaN	B: -0.38 to +0.78	C: +3.81 to +17.59	NaN	NaN

Learning of network parameters

In pgmpy it is possible to learn the CPT of a given Bayesian network using either a Bayesian Estimator or a Maximum Likelihood Estimator (MLE). The former exploits a known prior distribution of data, the latter does not make any particular assumption.

MLE can overfit the data in case of small datasets, because there can be not enough observations and thus the observed frequencies can be not representative. Another problem with MLE is the fact that state counts are done conditionally for each parents configuration and this causes immense fragmentation since the state counts drop even more. The Bayesian estimator instead does not only rely on input data to learn the network parameters, but it also takes advantage of a prior knowledge, expressed through a prior distribution. In this way, the estimator does not have an absolute guide, but rather a reasonable starting assumption that allows to counterbalance the lack of data.

Although the MLE approach seems plausible, it can be overly simplistic in many cases, whereas the Bayesian one is intrinsically more robust. As a consequence the Bayesian estimator is choosen.

There are several prior distribuitions available in pgmpy, a sensible choice of prior is the Bayesian Dirichlet equivalent uniform prior (BDeu). In the learning process, using BDeu, N uniform samples are generated for each variable to compute the pseudo-counts (default is N=5), hence the estimated probabilities in CPT are more conservative than the ones obtained through MLE (i.e. probabilities close to 1 or 0 get smoothed).

In the following cell the CPT are learned and displayed.

from pgmpy.estimators import BayesianEstimator, MaximumLikelihoodEstimator
from IPython.core.display import display, HTML

# disable text wrapping in output cell
display(HTML("<style>div.output_area pre {white-space: pre;}</style>"))

model.cpds = []
model.fit(data=df,
          estimator=BayesianEstimator,
          prior_type="BDeu",
          equivalent_sample_size=10,
          complete_samples_only=False)

print(f'Check model: {model.check_model()}\n')
for cpd in model.get_cpds():
    print(f'CPT of {cpd.variable}:')
    print(cpd, '\n')

Check model: True

CPT of Pop:
+------------------------+----------+
| Pop(A: -0.19 to +0.07) | 0.338164 |
+------------------------+----------+
| Pop(B: +0.07 to +0.50) | 0.338164 |
+------------------------+----------+
| Pop(C: +0.50 to +1.99) | 0.323671 |
+------------------------+----------+

CPT of EC:
+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+
| GDP                    | GDP(A: -5.71 to +1.24) | GDP(A: -5.71 to +1.24) | GDP(A: -5.71 to +1.24) | GDP(A: -5.71 to +1.24) | GDP(A: -5.71 to +1.24) | GDP(A: -5.71 to +1.24) | GDP(A: -5.71 to +1.24) | GDP(A: -5.71 to +1.24) | GDP(A: -5.71 to +1.24) | GDP(B: +1.24 to +2.89) | GDP(B: +1.24 to +2.89) | GDP(B: +1.24 to +2.89) | GDP(B: +1.24 to +2.89) | GDP(B: +1.24 to +2.89) | GDP(B: +1.24 to +2.89) | GDP(B: +1.24 to +2.89) | GDP(B: +1.24 to +2.89) | GDP(B: +1.24 to +2.89) | GDP(C: +2.89 to +7.49) | GDP(C: +2.89 to +7.49) | GDP(C: +2.89 to +7.49) | GDP(C: +2.89 to +7.49) | GDP(C: +2.89 to +7.49) | GDP(C: +2.89 to +7.49) | GDP(C: +2.89 to +7.49) | GDP(C: +2.89 to +7.49) | GDP(C: +2.89 to +7.49) |
+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+
| Pop                    | Pop(A: -0.19 to +0.07) | Pop(A: -0.19 to +0.07) | Pop(A: -0.19 to +0.07) | Pop(B: +0.07 to +0.50) | Pop(B: +0.07 to +0.50) | Pop(B: +0.07 to +0.50) | Pop(C: +0.50 to +1.99) | Pop(C: +0.50 to +1.99) | Pop(C: +0.50 to +1.99) | Pop(A: -0.19 to +0.07) | Pop(A: -0.19 to +0.07) | Pop(A: -0.19 to +0.07) | Pop(B: +0.07 to +0.50) | Pop(B: +0.07 to +0.50) | Pop(B: +0.07 to +0.50) | Pop(C: +0.50 to +1.99) | Pop(C: +0.50 to +1.99) | Pop(C: +0.50 to +1.99) | Pop(A: -0.19 to +0.07) | Pop(A: -0.19 to +0.07) | Pop(A: -0.19 to +0.07) | Pop(B: +0.07 to +0.50) | Pop(B: +0.07 to +0.50) | Pop(B: +0.07 to +0.50) | Pop(C: +0.50 to +1.99) | Pop(C: +0.50 to +1.99) | Pop(C: +0.50 to +1.99) |
+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+
| Urb                    | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) | Urb(A: -0.02 to +0.15) | Urb(B: +0.15 to +0.82) | Urb(C: +0.82 to +2.84) |
+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+
| EC(A: -7.05 to -0.12)  | 0.9435028248587572     | 0.09009009009009006    | 0.3333333333333333     | 0.8198198198198197     | 0.6120943952802359     | 0.3333333333333333     | 0.3333333333333333     | 0.09009009009009006    | 0.9435028248587572     | 0.13421828908554573    | 0.3333333333333333     | 0.3333333333333333     | 0.05208333333333332    | 0.4858757062146893     | 0.8198198198198197     | 0.3333333333333333     | 0.3333333333333333     | 0.052083333333333336   | 0.02824858757062147    | 0.3333333333333333     | 0.3333333333333333     | 0.09009009009009009    | 0.3333333333333333     | 0.3333333333333333     | 0.3333333333333333     | 0.3333333333333333     | 0.010857763300760043   |
+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+
| EC(B: -0.12 to +2.79)  | 0.028248587570621472   | 0.8198198198198197     | 0.3333333333333333     | 0.09009009009009006    | 0.2536873156342183     | 0.3333333333333333     | 0.3333333333333333     | 0.8198198198198197     | 0.028248587570621472   | 0.7315634218289085     | 0.3333333333333333     | 0.3333333333333333     | 0.8958333333333333     | 0.4858757062146893     | 0.09009009009009006    | 0.3333333333333333     | 0.3333333333333333     | 0.052083333333333336   | 0.7146892655367232     | 0.3333333333333333     | 0.3333333333333333     | 0.09009009009009009    | 0.036630036630036625   | 0.3333333333333333     | 0.3333333333333333     | 0.3333333333333333     | 0.09880564603691641    |
+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+
| EC(C: +2.79 to +13.06) | 0.028248587570621472   | 0.09009009009009006    | 0.3333333333333333     | 0.09009009009009006    | 0.13421828908554573    | 0.3333333333333333     | 0.3333333333333333     | 0.09009009009009006    | 0.028248587570621472   | 0.13421828908554573    | 0.3333333333333333     | 0.3333333333333333     | 0.05208333333333332    | 0.02824858757062147    | 0.09009009009009006    | 0.3333333333333333     | 0.3333333333333333     | 0.8958333333333335     | 0.2570621468926554     | 0.3333333333333333     | 0.3333333333333333     | 0.8198198198198199     | 0.63003663003663       | 0.3333333333333333     | 0.3333333333333333     | 0.3333333333333333     | 0.8903365906623236     |
+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+------------------------+

CPT of Urb:
+------------------------+----------+
| Urb(A: -0.02 to +0.15) | 0.338164 |
+------------------------+----------+
| Urb(B: +0.15 to +0.82) | 0.338164 |
+------------------------+----------+
| Urb(C: +0.82 to +2.84) | 0.323671 |
+------------------------+----------+

CPT of GDP:
+------------------------+----------+
| GDP(A: -5.71 to +1.24) | 0.343137 |
+------------------------+----------+
| GDP(B: +1.24 to +2.89) | 0.328431 |
+------------------------+----------+
| GDP(C: +2.89 to +7.49) | 0.328431 |
+------------------------+----------+

CPT of FFEC:
+-------------------------+-----------------------+-----------------------+------------------------+
| EC                      | EC(A: -7.05 to -0.12) | EC(B: -0.12 to +2.79) | EC(C: +2.79 to +13.06) |
+-------------------------+-----------------------+-----------------------+------------------------+
| FFEC(A: -2.72 to -0.40) | 0.5870646766169154    | 0.3333333333333333    | 0.09895833333333334    |
+-------------------------+-----------------------+-----------------------+------------------------+
| FFEC(B: -0.40 to +0.16) | 0.36318407960199006   | 0.4270833333333333    | 0.19270833333333331    |
+-------------------------+-----------------------+-----------------------+------------------------+
| FFEC(C: +0.16 to +2.34) | 0.04975124378109453   | 0.23958333333333331   | 0.7083333333333334     |
+-------------------------+-----------------------+-----------------------+------------------------+

CPT of REC:
+--------------------------+-----------------------+-----------------------+------------------------+
| EC                       | EC(A: -7.05 to -0.12) | EC(B: -0.12 to +2.79) | EC(C: +2.79 to +13.06) |
+--------------------------+-----------------------+-----------------------+------------------------+
| REC(A: -14.97 to +2.03)  | 0.2028985507246377    | 0.49612403100775193   | 0.3958333333333333     |
+--------------------------+-----------------------+-----------------------+------------------------+
| REC(B: +2.03 to +11.51)  | 0.3333333333333333    | 0.2868217054263566    | 0.3958333333333333     |
+--------------------------+-----------------------+-----------------------+------------------------+
| REC(C: +11.51 to +23.95) | 0.463768115942029     | 0.2170542635658915    | 0.20833333333333331    |
+--------------------------+-----------------------+-----------------------+------------------------+

CPT of EI:
+-----------------------+-----------------------+-----------------------+------------------------+
| EC                    | EC(A: -7.05 to -0.12) | EC(B: -0.12 to +2.79) | EC(C: +2.79 to +13.06) |
+-----------------------+-----------------------+-----------------------+------------------------+
| EI(A: -3.27 to -0.38) | 0.6766169154228856    | 0.2864583333333333    | 0.052083333333333336   |
+-----------------------+-----------------------+-----------------------+------------------------+
| EI(B: -0.38 to +0.78) | 0.2288557213930348    | 0.4739583333333333    | 0.2864583333333333     |
+-----------------------+-----------------------+-----------------------+------------------------+
| EI(C: +0.78 to +5.75) | 0.09452736318407962   | 0.23958333333333331   | 0.6614583333333334     |
+-----------------------+-----------------------+-----------------------+------------------------+

CPT of CO2:
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| FFEC                    | FFEC(A: -2.72 to -0.40) | FFEC(A: -2.72 to -0.40) | FFEC(A: -2.72 to -0.40)  | FFEC(B: -0.40 to +0.16) | FFEC(B: -0.40 to +0.16) | FFEC(B: -0.40 to +0.16)  | FFEC(C: +0.16 to +2.34) | FFEC(C: +0.16 to +2.34) | FFEC(C: +0.16 to +2.34)  |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| REC                     | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| CO2(A: -10.20 to -0.79) | 0.3333333333333333      | 0.463768115942029       | 0.6991869918699187       | 0.3333333333333333      | 0.463768115942029       | 0.3333333333333333       | 0.11904761904761905     | 0.3333333333333333      | 0.3333333333333333       |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| CO2(B: -0.79 to +3.81)  | 0.3333333333333333      | 0.463768115942029       | 0.26016260162601623      | 0.6145833333333334      | 0.463768115942029       | 0.3333333333333333       | 0.44047619047619047     | 0.3333333333333333      | 0.3333333333333333       |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| CO2(C: +3.81 to +17.59) | 0.3333333333333333      | 0.07246376811594203     | 0.04065040650406504      | 0.052083333333333336    | 0.07246376811594203     | 0.3333333333333333       | 0.44047619047619047     | 0.3333333333333333      | 0.3333333333333333       |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+

CPT of CH4:
+------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| FFEC                   | FFEC(A: -2.72 to -0.40) | FFEC(A: -2.72 to -0.40) | FFEC(A: -2.72 to -0.40)  | FFEC(B: -0.40 to +0.16) | FFEC(B: -0.40 to +0.16) | FFEC(B: -0.40 to +0.16)  | FFEC(C: +0.16 to +2.34) | FFEC(C: +0.16 to +2.34) | FFEC(C: +0.16 to +2.34)  |
+------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| REC                    | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) |
+------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| CH4(A: -6.02 to -0.31) | 0.3333333333333333      | 0.5765765765765766      | 0.22424242424242424      | 0.855072463768116       | 0.6594202898550725      | 0.3333333333333333       | 0.761904761904762       | 0.3333333333333333      | 0.3333333333333333       |
+------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| CH4(B: -0.31 to +2.11) | 0.3333333333333333      | 0.3333333333333333      | 0.7151515151515152       | 0.07246376811594203     | 0.2681159420289855      | 0.3333333333333333       | 0.11904761904761905     | 0.3333333333333333      | 0.3333333333333333       |
+------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| CH4(C: +2.11 to +9.00) | 0.3333333333333333      | 0.0900900900900901      | 0.06060606060606061      | 0.07246376811594203     | 0.07246376811594203     | 0.3333333333333333       | 0.11904761904761905     | 0.3333333333333333      | 0.3333333333333333       |
+------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+

CPT of N2O:
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| FFEC                    | FFEC(A: -2.72 to -0.40) | FFEC(A: -2.72 to -0.40) | FFEC(A: -2.72 to -0.40)  | FFEC(B: -0.40 to +0.16) | FFEC(B: -0.40 to +0.16) | FFEC(B: -0.40 to +0.16)  | FFEC(C: +0.16 to +2.34) | FFEC(C: +0.16 to +2.34) | FFEC(C: +0.16 to +2.34)  |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| REC                     | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) | REC(A: -14.97 to +2.03) | REC(B: +2.03 to +11.51) | REC(C: +11.51 to +23.95) |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| N2O(A: -4.31 to +0.61)  | 0.3333333333333333      | 0.5765765765765766      | 0.7151515151515152       | 0.463768115942029       | 0.07246376811594203     | 0.3333333333333333       | 0.11904761904761905     | 0.3333333333333333      | 0.3333333333333333       |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| N2O(B: +0.61 to +2.75)  | 0.3333333333333333      | 0.3333333333333333      | 0.06060606060606061      | 0.2681159420289855      | 0.6594202898550725      | 0.3333333333333333       | 0.11904761904761905     | 0.3333333333333333      | 0.3333333333333333       |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+
| N2O(C: +2.75 to +12.61) | 0.3333333333333333      | 0.0900900900900901      | 0.22424242424242424      | 0.2681159420289855      | 0.2681159420289855      | 0.3333333333333333       | 0.761904761904762       | 0.3333333333333333      | 0.3333333333333333       |
+-------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+-------------------------+-------------------------+--------------------------+

Network analysis

Among all the features, in pgmpy it is possible to investigate several properties of the network. For instance, it is possible to check for conditional independencies and active trails with respect to some given evidence or to ask for the Markov blanket of a node.

print(f'There can be made {len(model.get_independencies().get_assertions())}',
      'valid independence assertions with respect to the all possible given evidence.')
print('For instance, any node in the network is independent of its non-descendents given its parents (local semantics):\n',
      f'\n{model.local_independencies(nodes)}\n')

def active_trails_of(query, evidence):
    active = model.active_trail_nodes(query, observed=evidence).get(query)
    active.remove(query)
    if active:
        if evidence:
            print(f'Active trails between \'{query}\' and {active} given the evidence {set(evidence)}.')
        else:
            print(f'Active trails between \'{query}\' and {active} given no evidence.')
    else:
        print(f'No active trails for \'{query}\' given the evidence {set(evidence)}.')

def markov_blanket_of(node):
    print(f'Markov blanket of \'{node}\' is {set(model.get_markov_blanket(node))}')

active_trails_of(query='FFEC', evidence=[])
active_trails_of(query='FFEC', evidence=['EC'])
active_trails_of(query='FFEC', evidence=['EC', 'CO2'])
active_trails_of(query='EI', evidence=['EC'])
active_trails_of(query='CH4', evidence=['EC', 'FFEC'])
print()
markov_blanket_of(node='Pop')
markov_blanket_of(node='EC')
markov_blanket_of(node='REC')
markov_blanket_of(node='CH4') # note: a bug in pgmpy 0.1.10 raise a KeyError here.
                              # I opened an issue and I got accepted my pull request with the bug fix:
                              # https://github.com/pgmpy/pgmpy/issues/1293
                              # https://github.com/pgmpy/pgmpy/pull/1294

There can be made 2759 valid independence assertions with respect to the all possible given evidence.
For instance, any node in the network is independent of its non-descendents given its parents (local semantics):

(Pop _|_ GDP, Urb)
(Urb _|_ Pop, GDP)
(GDP _|_ Pop, Urb)
(FFEC _|_ EI, Pop, REC, GDP, Urb | EC)
(REC _|_ EI, Pop, FFEC, GDP, Urb | EC)
(EI _|_ N2O, REC, GDP, Urb, CO2, Pop, FFEC, CH4 | EC)
(CO2 _|_ N2O, EI, Pop, Urb, GDP, CH4, EC | FFEC, REC)
(CH4 _|_ N2O, EI, Pop, Urb, GDP, CO2, EC | FFEC, REC)
(N2O _|_ EI, Pop, Urb, GDP, CO2, CH4, EC | FFEC, REC)

Active trails between 'FFEC' and {'N2O', 'REC', 'Urb', 'GDP', 'CO2', 'EI', 'Pop', 'CH4', 'EC'} given no evidence.
Active trails between 'FFEC' and {'CO2', 'CH4', 'N2O'} given the evidence {'EC'}.
Active trails between 'FFEC' and {'CH4', 'N2O', 'REC'} given the evidence {'CO2', 'EC'}.
No active trails for 'EI' given the evidence {'EC'}.
Active trails between 'CH4' and {'CO2', 'N2O', 'REC'} given the evidence {'FFEC', 'EC'}.

Markov blanket of 'Pop' is {'Urb', 'GDP', 'EC'}
Markov blanket of 'EC' is {'REC', 'GDP', 'Urb', 'EI', 'Pop', 'FFEC'}
Markov blanket of 'REC' is {'N2O', 'CO2', 'FFEC', 'CH4', 'EC'}
Markov blanket of 'CH4' is {'FFEC', 'REC'}

The independence assertions, such as 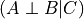, are implemented in pgmpy with the class IndependenceAssertion, which has 3 fields:

• event1: random variable which is independent (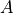 in the example).

• event2: random variables from which event1 is independent (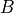 in the example).

• event3: random variables given which event1 is independent of event2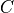 ( in the example).

In the following cell it is evaluated which are the nodes that have the maximum and the minimum number of appearance in independence assertions as independent variable or evidence. It can be notice that the closer a node is to the core of the network, the less are the independence assertions in which it is the independent variable and the more are the ones in which it is given as evidence.

def independent_assertions_score_function(node):
    return len([a for a in model.get_independencies().get_assertions() if node in a.event1])

def evidence_assertions_score_function(node):
    return len([a for a in model.get_independencies().get_assertions() if node in a.event3])

def update(assertion_dict, node, score_function):
    tmp_score = score_function(node)
    if tmp_score == assertion_dict["max"]["score"]:
        assertion_dict["max"]["nodes"].append(node)
    elif tmp_score > assertion_dict["max"]["score"]:
        assertion_dict["max"]["nodes"] = [node]
        assertion_dict["max"]["score"] = tmp_score
    if tmp_score == assertion_dict["min"]["score"]:
        assertion_dict["min"]["nodes"].append(node)
    elif tmp_score < assertion_dict["min"]["score"]:
        assertion_dict["min"]["nodes"] = [node]
        assertion_dict["min"]["score"] = tmp_score

if len(nodes) > 1:
    independent_init = independent_assertions_score_function(nodes[0])
    independent_dict = {"max": {"nodes": [nodes[0]], "score": independent_init},
                       "min": {"nodes": [nodes[0]], "score": independent_init}}
    evidence_init = evidence_assertions_score_function(nodes[0])
    evidence_dict = {"max": {"nodes": [nodes[0]], "score": evidence_init},
                    "min": {"nodes": [nodes[0]], "score": evidence_init}}
    for node in nodes[1:]:
        update(independent_dict, node, independent_assertions_score_function)
        update(evidence_dict, node, evidence_assertions_score_function)

print(f'Nodes which appear most ({independent_dict["max"]["score"]} times) in independence assertions',
      f'as independent variable are:\n{set(independent_dict["max"]["nodes"])}')
print(f'Nodes which appear least ({independent_dict["min"]["score"]} times) in independence assertions',
      f'as independent variable are:\n{set(independent_dict["min"]["nodes"])}')
print(f'Nodes which appear most ({evidence_dict["max"]["score"]} times) in independence assertions',
      f'as evidence are:\n{set(evidence_dict["max"]["nodes"])}')
print(f'Nodes which appear least ({evidence_dict["min"]["score"]} times) in independence assertions',
      f'as evidence are:\n{set(evidence_dict["min"]["nodes"])}')

Nodes which appear most (311 times) in independence assertions as independent variable are:
{'EI', 'Pop', 'GDP', 'Urb'}
Nodes which appear least (112 times) in independence assertions as independent variable are:
{'EC'}
Nodes which appear most (2222 times) in independence assertions as evidence are:
{'EC'}
Nodes which appear least (1179 times) in independence assertions as evidence are:
{'EI'}

Some queries on independence assertions are proposed.

from pgmpy.independencies.Independencies import IndependenceAssertion

def check_assertion(model, independent, from_variables, evidence):
    assertion = IndependenceAssertion(independent, from_variables, evidence)
    result = False
    for a in model.get_independencies().get_assertions():
        if frozenset(assertion.event1) == a.event1 and assertion.event2 <= a.event2 and frozenset(assertion.event3) == a.event3:
            result = True
            break
    print(f'{assertion}: {result}')

check_assertion(model, independent=['EI'], from_variables=['N2O'], evidence=['EC'])
check_assertion(model, independent=['EI'], from_variables=["FFEC", "REC", "GDP", "Pop", "Urb"], evidence=['EC'])
check_assertion(model, independent=['EC'], from_variables=["CH4"], evidence=['FFEC'])
check_assertion(model, independent=['EC'], from_variables=["CH4"], evidence=['FFEC', 'REC'])
check_assertion(model, independent=['FFEC'], from_variables=["REC"], evidence=['EC'])
check_assertion(model, independent=['FFEC'], from_variables=["REC"], evidence=['EC', 'CO2'])
check_assertion(model, independent=['CH4'], from_variables=["CO2"], evidence=['FFEC'])
check_assertion(model, independent=['CH4'], from_variables=["CO2"], evidence=['FFEC', 'REC'])

(EI _|_ N2O | EC): True
(EI _|_ REC, Urb, GDP, Pop, FFEC | EC): True
(EC _|_ CH4 | FFEC): False
(EC _|_ CH4 | FFEC, REC): True
(FFEC _|_ REC | EC): True
(FFEC _|_ REC | CO2, EC): False
(CH4 _|_ CO2 | FFEC): False
(CH4 _|_ CO2 | FFEC, REC): True

Inferences

In pgmpy it is possible to perform inference on a Bayesian network through the Variable Elimination method. The elimination order is evaluated through heuristic functions, which assign an elimination cost to each node that has to be removed (i.e. to each node apart from the query nodes and the evidence nodes). The variable elimination algorithm is then executed accordingly with the assigned node costs.

The available heuristic functions assign the cost of a node as:

• MinFill: the number of edges that need to be added to the graph due to its elimination.

• MinNeighbors: the number of neighbors it has in the current graph.

• MinWeight: the product of weights, domain cardinality, of its neighbors.

• WeightedMinFill: the sum of weights of the edges that need to be added to the graph due to its elimination, where a weight of an edge is the product of the weights, domain cardinality, of its constituent vertices.

The following cell is dedicated to inference queries and experiments on the cost heuristic functions.

from pgmpy.inference import VariableElimination
import time

def query_report(infer, variables, evidence=None, elimination_order="MinFill", show_progress=False, desc=""):
    if desc:
        print(desc)
    start_time = time.time()
    print(infer.query(variables=variables,
                      evidence=evidence,
                      elimination_order=elimination_order,
                      show_progress=show_progress))
    print(f'--- Query executed in {time.time() - start_time:0,.4f} seconds ---\n')

def get_ordering(infer, variables, evidence=None, elimination_order="MinFill", show_progress=False, desc=""):
    start_time = time.time()
    ordering = infer._get_elimination_order(variables=variables,
                                        evidence=evidence,
                                        elimination_order=elimination_order,
                                        show_progress=show_progress)
    if desc:
        print(desc, ordering, sep='\n')
        print(f'--- Ordering found in {time.time() - start_time:0,.4f} seconds ---\n')
    return ordering

def padding(heuristic):
    return (heuristic + ":").ljust(16)

def compare_all_ordering(infer, variables, evidence=None, show_progress=False):
    ord_dict = {
        "MinFill": get_ordering(infer, variables, evidence, "MinFill", show_progress),
        "MinNeighbors": get_ordering(infer, variables, evidence, "MinNeighbors", show_progress),
        "MinWeight": get_ordering(infer, variables, evidence, "MinWeight", show_progress),
        "WeightedMinFill": get_ordering(infer, variables, evidence, "WeightedMinFill", show_progress)
    }
    if not evidence:
        pre = f'elimination order found for probability query of {variables} with no evidence:'
    else:
        pre = f'elimination order found for probability query of {variables} with evidence {evidence}:'
    if ord_dict["MinFill"] == ord_dict["MinNeighbors"] and ord_dict["MinFill"] == ord_dict["MinWeight"] and ord_dict["MinFill"] == ord_dict["WeightedMinFill"]:
        print(f'All heuristics find the same {pre}.\n{ord_dict["MinFill"]}\n')
    else:
        print(f'Different {pre}')
        for heuristic, order in ord_dict.items():
            print(f'{padding(heuristic)} {order}')
        print()

infer = VariableElimination(model)

var = ['GDP']
heuristic = "MinNeighbors"
ordering = get_ordering(infer, variables=var, elimination_order=heuristic,
                        desc=f'Elimination order for {var} with no evidence computed through {heuristic} heuristic:')
query_report(infer, variables=var, elimination_order=ordering,
             desc=f'Probability query of {var} with no evidence through precomputed elimination order:')
query_report(infer, variables=var, elimination_order=list(reversed(ordering)),
             desc=f'Probability query of {var} with no evidence through dummy elimination order:')
compare_all_ordering(infer, variables=var)

var = ['CO2']
ev = {'EC': 'A: -7.05 to -0.12'}
heuristic = "MinFill"
query_report(infer, variables=var, evidence=ev, elimination_order=heuristic,
             desc=f'Probability query of {var} with evidence {ev} computed through {heuristic} heuristic:')
compare_all_ordering(infer, variables=var, evidence=ev)
heuristic = "MinNeighbors"
query_report(infer, variables=var, evidence=ev, elimination_order=heuristic,
             desc=f'Probability query of {var} with evidence {ev} computed through {heuristic} heuristic:')

Elimination order for ['GDP'] with no evidence computed through MinNeighbors heuristic:
['EI', 'N2O', 'CO2', 'CH4', 'REC', 'FFEC', 'Urb', 'Pop', 'EC']
--- Ordering found in 0.0022 seconds ---

Probability query of ['GDP'] with no evidence through precomputed elimination order:
+------------------------+------------+
| GDP                    |   phi(GDP) |
+========================+============+
| GDP(A: -5.71 to +1.24) |     0.3431 |
+------------------------+------------+
| GDP(B: +1.24 to +2.89) |     0.3284 |
+------------------------+------------+
| GDP(C: +2.89 to +7.49) |     0.3284 |
+------------------------+------------+
--- Query executed in 0.0196 seconds ---

Probability query of ['GDP'] with no evidence through dummy elimination order:
+------------------------+------------+
| GDP                    |   phi(GDP) |
+========================+============+
| GDP(A: -5.71 to +1.24) |     0.3431 |
+------------------------+------------+
| GDP(B: +1.24 to +2.89) |     0.3284 |
+------------------------+------------+
| GDP(C: +2.89 to +7.49) |     0.3284 |
+------------------------+------------+
--- Query executed in 0.1300 seconds ---

Different elimination order found for probability query of ['GDP'] with no evidence:
MinFill:         ['N2O', 'Urb', 'CO2', 'REC', 'EI', 'Pop', 'FFEC', 'CH4', 'EC']
MinNeighbors:    ['EI', 'N2O', 'CO2', 'CH4', 'REC', 'FFEC', 'Urb', 'Pop', 'EC']
MinWeight:       ['EI', 'N2O', 'CO2', 'CH4', 'REC', 'FFEC', 'Urb', 'Pop', 'EC']
WeightedMinFill: ['EI', 'N2O', 'CO2', 'CH4', 'REC', 'FFEC', 'Urb', 'Pop', 'EC']

Probability query of ['CO2'] with evidence {'EC': 'A: -7.05 to -0.12'} computed through MinFill heuristic:
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.4721 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.3765 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.1514 |
+-------------------------+------------+
--- Query executed in 0.0237 seconds ---

Different elimination order found for probability query of ['CO2'] with evidence {'EC': 'A: -7.05 to -0.12'}:
MinFill:         ['N2O', 'GDP', 'Urb', 'EI', 'Pop', 'CH4', 'REC', 'FFEC']
MinNeighbors:    ['EI', 'N2O', 'CH4', 'REC', 'FFEC', 'GDP', 'Urb', 'Pop']
MinWeight:       ['EI', 'N2O', 'CH4', 'REC', 'FFEC', 'GDP', 'Urb', 'Pop']
WeightedMinFill: ['EI', 'N2O', 'CH4', 'REC', 'FFEC', 'GDP', 'Urb', 'Pop']

Probability query of ['CO2'] with evidence {'EC': 'A: -7.05 to -0.12'} computed through MinNeighbors heuristic:
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.4721 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.3765 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.1514 |
+-------------------------+------------+
--- Query executed in 0.0302 seconds ---

This last part of this document try to answer to some key questions using probability queries about the greenhouse gases scenario:

• a considerable population growth lead to an increase of energy consumption and CO2 diffusion

• an increase of urbanization growth rate and GDP per capita are important factors in CO2 diffusion

• energy consumption reduction lead to CO2 diffusion reduction

• an increase of CO2 diffusion is evidence of an increase of CH4 and N2O diffusion

• a reduction of CO2 diffusion is evidence of a reduction of CH4 and N2O diffusion

• fossil fuel consumption reduction and renewable energy consumption increase impact significantly on greenhouse gases diffusion.

query_report(infer, variables=['EC'], evidence={'Pop': 'C: +0.50 to +1.99'},
             desc='Probability of energy consumption increase with population growth over +0.50%:')
query_report(infer, variables=['CO2'], evidence={'Pop': 'C: +0.50 to +1.99'},
             desc='Probability of CO2 increase with population growth over +0.50%:')
query_report(infer, variables=['CO2'], evidence={'Urb': 'C: +0.82 to +2.84'},
             desc='Probability of CO2 increase with urbanization growth over +0.82%:')
query_report(infer, variables=['CO2'], evidence={'GDP': 'C: +2.89 to +7.49'},
             desc='Probability of CO2 increase with GDP per capita growth over +2.89%:')
query_report(infer, variables=['CO2'],
             evidence={'Pop': 'C: +0.50 to +1.99', 'Urb': 'C: +0.82 to +2.84', 'GDP': 'C: +2.89 to +7.49'},
             desc='Probability of CO2 increase with:\n - population growth over +0.50%\n - urbanization growth over +0.82%\n - GDP per capita growth over +2.89%:')
query_report(infer, variables=['CO2'], evidence={'EC': 'A: -7.05 to -0.12'},
             desc='Probability of CO2 increase with energy consumption growth under -0.12%:')
query_report(infer, variables=['CO2'], evidence={'EC': 'C: +2.79 to +13.06'},
             desc='Probability of CO2 increase with energy consumption growth over +2.79%:')
query_report(infer, variables=['CH4'], evidence={'CO2': 'C: +3.81 to +17.59'},
             desc='Probability of CH4 increase with CO2 growth over +3.81%:')
query_report(infer, variables=['CH4'], evidence={'CO2': 'A: -10.20 to -0.79'},
             desc='Probability of CH4 increase with CO2 growth under -0.79%:')
query_report(infer, variables=['CH4'],
             desc='Probability of CH4 increase with no given evidence:')
query_report(infer, variables=['N2O'], evidence={'CO2': 'C: +3.81 to +17.59'},
             desc='Probability of N2O increase with CO2 growth over +3.81%:')
query_report(infer, variables=['N2O'], evidence={'CO2': 'A: -10.20 to -0.79'},
             desc='Probability of N2O increase with CO2 growth under -0.79%:')
query_report(infer, variables=['N2O'],
             desc='Probability of N2O increase with no given evidence:')
query_report(infer, variables=['FFEC', 'REC'],
             desc='Joint probability of fossil fuel energy consumption and renewable energy consumption:')
query_report(infer, variables=['CO2'], evidence={'FFEC': 'A: -2.72 to -0.40', 'REC': 'C: +11.51 to +23.95'},
             desc='Probability of CO2 increase with:\n - fossil fuel energy consumption growth under -0.40%\n - renewable energy consumption growth over +11.51%')
query_report(infer, variables=['CH4'], evidence={'FFEC': 'A: -2.72 to -0.40', 'REC': 'C: +11.51 to +23.95'},
             desc='Probability of CH4 increase with:\n - fossil fuel energy consumption growth under -0.40%\n - renewable energy consumption growth over +11.51%')
query_report(infer, variables=['N2O'], evidence={'FFEC': 'A: -2.72 to -0.40', 'REC': 'C: +11.51 to +23.95'},
             desc='Probability of N2O increase with:\n - fossil fuel energy consumption growth under -0.40%\n - renewable energy consumption growth over +11.51%')

Probability of energy consumption increase with population growth over +0.50%:
+------------------------+-----------+
| EC                     |   phi(EC) |
+========================+===========+
| EC(A: -7.05 to -0.12)  |    0.3087 |
+------------------------+-----------+
| EC(B: -0.12 to +2.79)  |    0.3011 |
+------------------------+-----------+
| EC(C: +2.79 to +13.06) |    0.3902 |
+------------------------+-----------+
--- Query executed in 0.0331 seconds ---

Probability of CO2 increase with population growth over +0.50%:
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.3704 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.4008 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.2288 |
+-------------------------+------------+
--- Query executed in 0.0276 seconds ---

Probability of CO2 increase with urbanization growth over +0.82%:
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.3793 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.3965 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.2242 |
+-------------------------+------------+
--- Query executed in 0.0253 seconds ---

Probability of CO2 increase with GDP per capita growth over +2.89%:
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.3570 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.4021 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.2409 |
+-------------------------+------------+
--- Query executed in 0.0234 seconds ---

Probability of CO2 increase with:
 - population growth over +0.50%
 - urbanization growth over +0.82%
 - GDP per capita growth over +2.89%:
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.3044 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.4011 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.2945 |
+-------------------------+------------+
--- Query executed in 0.0251 seconds ---

Probability of CO2 increase with energy consumption growth under -0.12%:
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.4721 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.3765 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.1514 |
+-------------------------+------------+
--- Query executed in 0.0320 seconds ---

Probability of CO2 increase with energy consumption growth over +2.79%:
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.2959 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.3984 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.3058 |
+-------------------------+------------+
--- Query executed in 0.0295 seconds ---

Probability of CH4 increase with CO2 growth over +3.81%:
+------------------------+------------+
| CH4                    |   phi(CH4) |
+========================+============+
| CH4(A: -6.02 to -0.31) |     0.4789 |
+------------------------+------------+
| CH4(B: -0.31 to +2.11) |     0.2765 |
+------------------------+------------+
| CH4(C: +2.11 to +9.00) |     0.2446 |
+------------------------+------------+
--- Query executed in 0.0279 seconds ---

Probability of CH4 increase with CO2 growth under -0.79%:
+------------------------+------------+
| CH4                    |   phi(CH4) |
+========================+============+
| CH4(A: -6.02 to -0.31) |     0.4573 |
+------------------------+------------+
| CH4(B: -0.31 to +2.11) |     0.3776 |
+------------------------+------------+
| CH4(C: +2.11 to +9.00) |     0.1650 |
+------------------------+------------+
--- Query executed in 0.0219 seconds ---

Probability of CH4 increase with no given evidence:
+------------------------+------------+
| CH4                    |   phi(CH4) |
+========================+============+
| CH4(A: -6.02 to -0.31) |     0.5014 |
+------------------------+------------+
| CH4(B: -0.31 to +2.11) |     0.3155 |
+------------------------+------------+
| CH4(C: +2.11 to +9.00) |     0.1831 |
+------------------------+------------+
--- Query executed in 0.0198 seconds ---

Probability of N2O increase with CO2 growth over +3.81%:
+-------------------------+------------+
| N2O                     |   phi(N2O) |
+=========================+============+
| N2O(A: -4.31 to +0.61)  |     0.2901 |
+-------------------------+------------+
| N2O(B: +0.61 to +2.75)  |     0.2807 |
+-------------------------+------------+
| N2O(C: +2.75 to +12.61) |     0.4292 |
+-------------------------+------------+
--- Query executed in 0.0220 seconds ---

Probability of N2O increase with CO2 growth under -0.79%:
+-------------------------+------------+
| N2O                     |   phi(N2O) |
+=========================+============+
| N2O(A: -4.31 to +0.61)  |     0.4274 |
+-------------------------+------------+
| N2O(B: +0.61 to +2.75)  |     0.2968 |
+-------------------------+------------+
| N2O(C: +2.75 to +12.61) |     0.2758 |
+-------------------------+------------+
--- Query executed in 0.0223 seconds ---

Probability of N2O increase with no given evidence:
+-------------------------+------------+
| N2O                     |   phi(N2O) |
+=========================+============+
| N2O(A: -4.31 to +0.61)  |     0.3699 |
+-------------------------+------------+
| N2O(B: +0.61 to +2.75)  |     0.2982 |
+-------------------------+------------+
| N2O(C: +2.75 to +12.61) |     0.3319 |
+-------------------------+------------+
--- Query executed in 0.0209 seconds ---

Joint probability of fossil fuel energy consumption and renewable energy consumption:
+--------------------------+-------------------------+-----------------+
| REC                      | FFEC                    |   phi(REC,FFEC) |
+==========================+=========================+=================+
| REC(A: -14.97 to +2.03)  | FFEC(A: -2.72 to -0.40) |          0.1110 |
+--------------------------+-------------------------+-----------------+
| REC(A: -14.97 to +2.03)  | FFEC(B: -0.40 to +0.16) |          0.1221 |
+--------------------------+-------------------------+-----------------+
| REC(A: -14.97 to +2.03)  | FFEC(C: +0.16 to +2.34) |          0.1290 |
+--------------------------+-------------------------+-----------------+
| REC(B: +2.03 to +11.51)  | FFEC(A: -2.72 to -0.40) |          0.1141 |
+--------------------------+-------------------------+-----------------+
| REC(B: +2.03 to +11.51)  | FFEC(B: -0.40 to +0.16) |          0.1081 |
+--------------------------+-------------------------+-----------------+
| REC(B: +2.03 to +11.51)  | FFEC(C: +0.16 to +2.34) |          0.1140 |
+--------------------------+-------------------------+-----------------+
| REC(C: +11.51 to +23.95) | FFEC(A: -2.72 to -0.40) |          0.1276 |
+--------------------------+-------------------------+-----------------+
| REC(C: +11.51 to +23.95) | FFEC(B: -0.40 to +0.16) |          0.1037 |
+--------------------------+-------------------------+-----------------+
| REC(C: +11.51 to +23.95) | FFEC(C: +0.16 to +2.34) |          0.0705 |
+--------------------------+-------------------------+-----------------+
--- Query executed in 0.0218 seconds ---

Probability of CO2 increase with:
 - fossil fuel energy consumption growth under -0.40%
 - renewable energy consumption growth over +11.51%
+-------------------------+------------+
| CO2                     |   phi(CO2) |
+=========================+============+
| CO2(A: -10.20 to -0.79) |     0.6992 |
+-------------------------+------------+
| CO2(B: -0.79 to +3.81)  |     0.2602 |
+-------------------------+------------+
| CO2(C: +3.81 to +17.59) |     0.0407 |
+-------------------------+------------+
--- Query executed in 0.0250 seconds ---

Probability of CH4 increase with:
 - fossil fuel energy consumption growth under -0.40%
 - renewable energy consumption growth over +11.51%
+------------------------+------------+
| CH4                    |   phi(CH4) |
+========================+============+
| CH4(A: -6.02 to -0.31) |     0.2242 |
+------------------------+------------+
| CH4(B: -0.31 to +2.11) |     0.7152 |
+------------------------+------------+
| CH4(C: +2.11 to +9.00) |     0.0606 |
+------------------------+------------+
--- Query executed in 0.0239 seconds ---

Probability of N2O increase with:
 - fossil fuel energy consumption growth under -0.40%
 - renewable energy consumption growth over +11.51%
+-------------------------+------------+
| N2O                     |   phi(N2O) |
+=========================+============+
| N2O(A: -4.31 to +0.61)  |     0.7152 |
+-------------------------+------------+
| N2O(B: +0.61 to +2.75)  |     0.0606 |
+-------------------------+------------+
| N2O(C: +2.75 to +12.61) |     0.2242 |
+-------------------------+------------+
--- Query executed in 0.0273 seconds ---

We can get the following outcomes from the queries on the modelled Bayesian network:

• Energy consumption vs Population, Urbanization, GDP: the increase of gases diffusion is more clearly proportional to energy consumption growth rather than population, urbanization or GDP per capita growth. This result can be a symptom that some important casual factors of the energy consumption growth strictly correlated with greenhouse gases diffusion, such as industrialization, are not represented into the network.

• N2O vs CH4: N2O growth trends almost resemble the ones of CO2, whereas the CH4 growth seems very likely to decrease regardless of the evidence. This is unlikely to be the real situation, and the probability query of CH4 without given evidence proves it: the lower tier ‘A’ is much more likely than the others, and that is a consequence of data sparsity. The other 2 tiers of CH4 are underrepresented. That is not the case of N2O, whose tiers are more balanced.

• Fossil fuel vs Renewable: finally and most importantly, the output probabilites of the last queries suggest that the reduction of fossil fuel energy consumption and the increase of renewable energy consumption are really effective strategies to minimize greenhouse gases emissions, hence it is really important to use sustainable energies.

[1] U.S. Environmental Protection Agency - Greenhouse Gas Emissions

[2] Didem Cinar, Gulgun Kayakutlu - Scenario analysis using Bayesian networks: A case study in energy sector

[3] World Bank Open Data